Inner product | Jiahui Chen

2.1 Dot Product, Norm, Distance, Orthogonal Vectors

Let $\mathbf{u},\mathbf{v} \in \mathbb R^n$ be given by $\mathbf{u}=[u_1, \dots u_n]$ and $\mathbf{v}=[v_1, \dots v_n]$, then their dot product is a scalar, mathematically denoted by $\mathbf{u}\cdot \mathbf{v}$ and is given by

$\mathbf{u}\cdot \mathbf{v} = \text{dot}(\mathbf{u},\mathbf{v}) = u_1v_1 + u_2v_2 +\dots + u_nv_n \in \mathbb R$.

Definition 1.

We say $\mathbf{u}$ is orthogonal to $\mathbf{v}$, if $\mathbf{u}\cdot \mathbf{v} =0$.

Definition 2.

Given a vector $\mathbf{u}$, the norm (length) of $\mathbf{u}$ is given by $||\mathbf{u}|| = \sqrt{\mathbf{u}\cdot \mathbf{u}}$.

Definition 3.

Given vectors $\mathbf{u}, \mathbf{v} \in \mathbb R^n$, the distance between $\mathbf{u}$ and $\mathbf{v}$ is given by $||\mathbf{u} - \mathbf{v}|| = \sqrt{(\mathbf{u}-\mathbf{v})\cdot (\mathbf{u}-\mathbf{v})}$.

Use Python to compute the dot product between $\mathbf{u} = [ 1, 7, 9, 11]$ and $\mathbf{v} = [ 7, 1, 2, 2]$ (Store the information in a variable called uv).

import numpy as np
u = [1,7,9,11]
v = [7,1,2,2]
uv = np.dot(u,v)
print(uv)

Given two vectors $\mathbf{u}$ and $\mathbf{v}$ in $\mathbb{R}^n$ (i.e. they have the same length), the “dot” product operation multiplies all of the corresponding elements and then adds them together. Ex:

$\mathbf{u} = [u_1, u_2, \dots, u_n]$ $\mathbf{v} = [v_1, v_2, \dots, v_n]$

\[\mathbf{u}\cdot \mathbf{v} = u_1 v_1 + u_2 v_2 + \dots + u_nv_n\]

or:

\[\mathbf{u}\cdot \mathbf{v} = \sum^n_{i=1} u_i v_i\]

This can easily be written as Python code as follows:

u = [1,2,3]
v = [3,2,1]
solution = 0
for i in range(len(u)):
    solution += u[i]*v[i]
    
solution

2.2 Inner Products

Definition: An inner product on a vector space $V$ (Remember that $\mathbb{R}^n$ is just one class of vector spaces) is a function that associates a number, denoted as $\langle \mathbf{u},\mathbf{v} \rangle$, with each pair of vectors $\mathbf{u}$ and $\mathbf{v}$ of $V$. This function satisfies the following conditions for vectors $\mathbf{u}, \mathbf{v}, \mathbf{w}$ and scalar $c$:

$\langle \mathbf{u},\mathbf{v} \rangle = \langle \mathbf{v},\mathbf{u} \rangle$ (symmetry axiom)
$\langle \mathbf{u}+\mathbf{v},\mathbf{w} \rangle = \langle \mathbf{u},\mathbf{w} \rangle + \langle \mathbf{v},\mathbf{w} \rangle$ (additive axiom)
$\langle c\mathbf{u},\mathbf{v} \rangle = c\langle \mathbf{u},\mathbf{v} \rangle$ (homogeneity axiom)
$\langle \mathbf{u},\mathbf{u} \rangle \ge 0 \text{ and } \langle \mathbf{u},\mathbf{u} \rangle = 0 \text{ if and only if } \mathbf{u} = 0$ (positive definite axiom)

The dot product of $\mathbb{R}^n$ is an inner product. Note that we can define new inner products for $\mathbb{R}^n$.

Here is an example of a non-standard inner product in $\mathbb{R}^n$:

Consider two vectors $\mathbf{x} = [x_1, x_2, \ldots, x_n]$ and $\mathbf{y} = [y_1, y_2, \ldots, y_n]$. A new inner product, denoted $\langle \mathbf{x}, \mathbf{y} \rangle'$, can be defined as:

\[\langle \mathbf{x}, \mathbf{y} \rangle' = \sum_{i=1}^{n} a_i x_i y_i\]

where $a_i > 0$ for all $i$ (i.e., $a_i$ are positive constants).

This new inner product is still bilinear (additive + homogeneity), symmetric, and positive-definite, which makes it a valid inner product.

For instance, let’s say $a_i = i$ for all $i$, the inner product of $\mathbf{x}$ and $\mathbf{y}$ becomes:

\[\langle \mathbf{x}, \mathbf{y} \rangle' = x_1 y_1 + 2 x_2 y_2 + 3 x_3 y_3 + \ldots + n x_n y_n\]

This is a perfectly valid inner product for vectors in $\mathbb{R}^n$, and it’s clearly different from the standard dot product.

Let $\mathbb{R}^2$ have an inner (dot) product defined by: $\langle (a_1,a_2),(b_1,b_2)\rangle = 2a_1b_1 + 3a_2b_2.$

Norm of a vector

Definition: Let $V$ be an inner product space. The norm of a vector $\mathbf{v}$ is denoted by $\| \mathbf{v} \|$ and is defined by:

\[\| \mathbf{v} \| = \sqrt{\langle \mathbf{v}, \mathbf{v} \rangle}.\]

Angle between two vectors

Definition: Let $V$ be a real inner product space. The angle $\theta$ between two nonzero vectors $\mathbf{u}$ and $\mathbf{v}$ in $V$ is given by:

\[cos(\theta) = \frac{\langle \mathbf{u}, \mathbf{v} \rangle}{\| \mathbf{u} \| \| \mathbf{v} \|}.\]

Orthogonal vectors

Definition: Let $V$ be an inner product space. Two vectors $\mathbf{u}$ and $\mathbf{v}$ in $V$ are orthogonal if their inner product is zero:

\[\langle \mathbf{u}, \mathbf{v} \rangle = 0.\]

Distance

Definition: Let $V$ be an inner product space. The distance between two vectors (points) $\mathbf{u}$ and $\mathbf{v}$ in $V$ is denoted by $d(\mathbf{u},\mathbf{v})$ and is defined by:

\[d(\mathbf{u},\mathbf{v}) = \| \mathbf{u}-\mathbf{v} \| = \sqrt{\langle \mathbf{u}-\mathbf{v}, \mathbf{u}-\mathbf{v} \rangle}\]

import numpy as np

# Define two complex vectors A and B
A = np.array([1 + 2j, 2 + 3j, 3 + 4j])
B = np.array([4 + 5j, 5 + 6j, 6 + 7j])
print("The conjugate of B:", np.conj(B))

# Calculate the inner product
inner_product = np.dot(A, np.conj(B))

print("The inner product is:", inner_product)

The conjugate of B: [4.-5.j 5.-6.j 6.-7.j]
The inner product is: (88+9j)

2.2.1 Inner Product on Functions

In functional analysis, an inner product on functions extends the concept of the dot product in finite-dimensional spaces to function spaces. Essentially, the inner product of two functions $f$ and $g$ is a complex number that provides a measure of the “similarity” between the two functions over a specified interval. The inner product of $f$ and $g$ in a Hilbert space (vector space) of square-integrable functions over an interval $[a, b]$ is commonly defined as:

\langle f, g \rangle = \int_{a}^{b} f(x) \overline{g(x)} \, dx

Here, $\overline{g(x)}$ is the complex conjugate of $g(x)$.

This definition generalizes the dot product and retains many of its essential properties, including commutativity, linearity, and the identification of orthogonal functions. In this framework, functions themselves can be considered as vectors in an infinite-dimensional Hilbert space, and the operations of vector addition and scalar multiplication are defined pointwise.

This concept is crucial for the study of various problems in mathematics, physics, and engineering, such as solving differential equations, quantum mechanics, and signal processing.

Example

Consider the following functions

$f(x)=3x-1$ $g(x)=5x+3$

with inner product defined by $\langle f,g\rangle=\int_0^1{f(x)\overline{g(x)}dx}.$

✅ QUESTION: What is the norm of $f(x)$ in this space?

from scipy.integrate import quad
import numpy as np

def f(x):
    return x

def g(x):
    return x ** 2

def inner_product(func1, func2, a, b):
    # Compute the integral of func1(x) * conj(func2(x)) from a to b
    result, _ = quad(lambda x: np.conj(func2(x)) * func1(x), a, b)
    return result

# Compute the inner product of f and g over the interval [0, 1]
result = inner_product(f, g, 0, 1)
print(f"The inner product is {result}")

The inner product is 0.25

2.3 Polynomial Approximation

Polynomial approximation is a critical topic in numerical analysis and applied mathematics. By approximating more complicated functions with simpler polynomial functions, we can solve or simplify many practical problems. In many scientific problems, it is desirable to approximate a complicated function by a simpler function. One common choice is to approximate the function of interest $f(x)$ by a low-degree polynomial. The set of all polynomials of degree less than or equal to $n$ forms a vector space $P_n$. Specifically, $P_n$ is the set of all functions of the form: $f(x) = a_0 + a_1x + a_2x^2 + \cdots + a_dx^d,$ where $a_0, a_1, \ldots, a_n$ are real numbers.

Vector Space Properties

A polynomial vector space retains all the fundamental properties of vector spaces:

Closure under addition: The sum of two polynomials in $P_n$ is also in $P_n$.
Closure under scalar multiplication: A polynomial in $P_n$ scaled by a scalar is also in $P_n$.
Existence of Zero Vector: The zero polynomial $f(x) = 0$ is in $P_n$.
Existence of Additive Inverses: For every polynomial $f(x)$ in $P_n$, there exists a polynomial $-f(x)$ in $P_n$ such that $f(x) + (-f(x)) = 0$.

Example: Vector Addition

For $f(x) = x + 1$ and $g(x) = x^2 - 1$ in $P_2$,

\[f(x) + g(x) = x^2 + x\]

The result is still a polynomial of degree less than or equal to 2, confirming closure under addition.

2.3.1 Least Squares Polynomial Approximation

Another approach to find an approximating polynomial is the method of least squares, which minimizes the error between the polynomial and the function being approximated.

Python Example

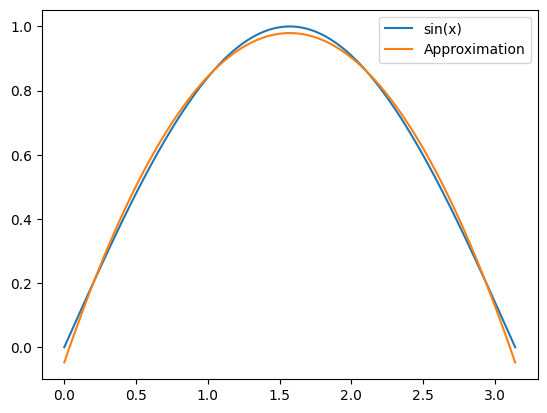
Here’s a Python example using NumPy to generate a least squares polynomial approximation of degree 2 for the function $f(x) = \sin(x)$ on the interval $[0, \pi]$. Change the variable degree to see how it converge to $\sin(x)$.

import numpy as np
import matplotlib.pyplot as plt

# Define the function and its domain
x = np.linspace(0, np.pi, 100)
y = np.sin(x)

# Fit a polynomial of degree 2 (quadratic)
degree = 2
coeff = np.polyfit(x, y, degree)

# Create the polynomial object
p = np.poly1d(coeff) # A one-dimensional polynomial class.

# Evaluate the polynomial at the points x
y_fit = p(x)

# Plot the function and its approximation
plt.plot(x, y, label='sin(x)')
plt.plot(x, y_fit, label='Approximation')
plt.legend()
plt.show()

2.3.2 Taylor’s Theorem

Introduction

Taylor’s Theorem provides a way to approximate functions by polynomials. When we can’t solve a function explicitly, or when it’s computationally expensive to do so, Taylor series can offer a viable alternative by presenting a polynomial that approximates the function closely within a certain range.

Theorem of Single Variable

If a function $f$ is $n$-times differentiable on an interval $I$ containing the point $a$, and $f^{(n+1)}(x)$ exists for each $x$ in $I$, then for each $x$ in $I$, there exists a number $\eta$ between $a$ and $x$ such that: $f(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + ... + \frac{f^{(n)}(a)}{n!}(x-a)^n + \frac{f^{(n+1)}(\eta)}{(n+1)!}(x-a)^{n+1}$

The first $n$ terms of this expansion constitute the $n$-th degree Taylor polynomial $T_n(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \ldots + \frac{f^{(n)}(a)}{n!}(x-a)^n$ for $f$ centered at $a$. The last term is the remainder, $R_n = \frac{f^{(n+1)}(\eta)}{(n+1)!}(x-a)^{n+1},$ which goes to zero faster than the largest power of $x - a$ as $x$ approaches $a$ if $f$ is $(n+1)$-times differentiable at $a$.

A different, but equivalent, way to write is $f(x+h) = f(x) + hf'(x) + \frac{h^2}{2!}f''(x) + \ldots + \frac{h^n}{n!}f^{(n)}(x) + R_n(x).$

Derivation

To derive the Taylor series expansion for a function $f(x)$ about the point $x = a$:

Zeroth Order Term: The value of the function at the point $a$: $f(a)$.
First Order Term: The first derivative gives the slope or rate of change of the function. By multiplying it with $(x - a)$, we determine the linear approximation of the function around the point $a$.
Higher Order Terms: Similarly, the second derivative gives the rate of change of the rate of change, or curvature. We take into account this curvature by including a term proportional to $(x - a)^2$, and so forth for higher-order terms.

This continues for as many derivatives as we know or require, with each term capturing more intricate details of the function’s behavior near $a$.

Examples

The expansion of $e^x$ about $x = 0$: $e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + ...$

The expansion of $\frac{1}{1-x}$ about $x =0$: $\frac{1}{1-x} = 1 + x + x^2 + x^3 + ...$

Theorem of Two Variables

The two-variable version of the expansion is $f(x+h, t+k) = f(x,t) +Df(x,t) + \frac{1}{2}D^2f(x,t) + ... + \frac{1}{n!}D^nf(x,t) + R_n$ where $D = h\frac{\partial}{\partial x} + k\frac{\partial}{\partial t}.$ Alternatively, writing this out yields $f(x+h, t+k) = f(x,t) + hf_x(x,t) + kf_t(x,t) + \frac{1}{2}h^2f_{xx}(x,t) + hkf_{xt}(x, t) + \frac{1}{2}k^2f_{tt}(x,t) + ...$ The subscripts in the above expression denote partial differentiation, such as $f_{xt}=\frac{\partial^2f}{\partial x\partial t}.$

2.3.3 Lagrange Interpolation

Lagrange Interpolation is another common method used for polynomial approximation. It’s designed to go through a specific set of points $(x_1, y_1), \ldots, (x_n, y_n)$ exactly.

The Lagrange polynomial $L(x)$ is given by:

\[L(x) = \sum_{i=1}^{n} y_i \cdot l_i(x)\]

where $l_i(x)$ are the Lagrange basis polynomials:

$l_i(x) = \prod_{j \neq i} \frac{x - x_j}{x_i - x_j}$

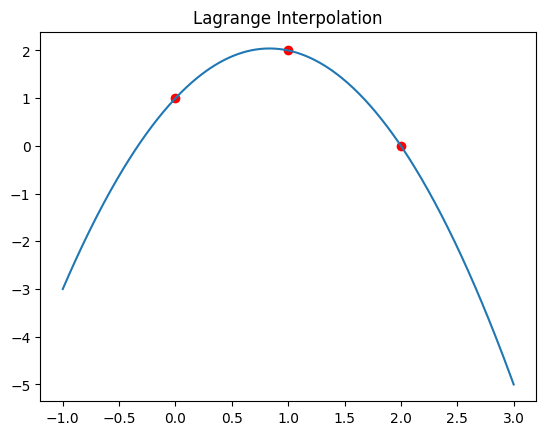
Python Example for Lagrange Interpolation

from scipy.interpolate import lagrange
import numpy as np
import matplotlib.pyplot as plt

# Sample points
x_points = np.array([0, 1, 2])
y_points = np.array([1, 2, 0])

# Lagrange interpolation
poly = lagrange(x_points, y_points)

# Evaluate polynomial
x = np.linspace(min(x_points) - 1, max(x_points) + 1, 400)
y = poly(x)

plt.scatter(x_points, y_points, color='red')
plt.plot(x, y)
plt.title('Lagrange Interpolation')
plt.show()

Other Polynomial Approximations

Legendre Polynomial: Used in spectral methods to create an orthogonal basis with which you can expand your solution.
Hermite Polynomial: A class of orthogonal polynomials that arise in probability theory, quantum mechanics, and numerical analysis, among other fields.
Newton’s Interpolating Polynomial: Useful when adding new data points, as you don’t have to recompute the entire polynomial.
Chebyshev Approximation: Uses Chebyshev polynomials to minimize the maximum error in approximation. Effective in approximating functions over a specific interval.
Bernstein Polynomial: Used in the field of computer graphics, particularly in the design of curves and surfaces.
Spline Interpolation: Instead of using a single high-degree polynomial, splines use lower-degree polynomials for each interval between data points, ensuring smoother and more controlled behavior.