On preconditioning the treecode-accelerated boundary integral Poisson-Boltzmann solver

This project works on a preconditioning scheme using preconditioner matrix \(M\) such that \(M^{-1}A\) has much improved condition while \(M^{-1}z\) can be rapidly computed for any vector \(z\). In this scheme, the matrix \(M\) carries the interactions between boundary elements on the same leaf only in the tree structure thus is block diagonal with many computational advantages. The sizes of the blocks in \(M\) are conveniently controlled by treecode parameter \(N_0\), the maximum number of particles per leaf. The numerical results show that this new preconditioning scheme improves the treecode-accelerated boundary integral (TABI) solver with significantly reduced iteration numbers and better accuracy, particularly for protein sets on which TABI solver previously converges slowly.

Treecode for electrostatic interactions

For a system of \(N\) particles located at \(\textbf{x}_i\) with partial charges \(q_{i}, i=1,\ldots,N\), we denote the induced potential at \(\textbf{x}_{i}\) by \begin{equation} \label{particle-particle} V_{i}=\sum_{j=1, j\neq i}^N q_{i}G(\textbf x_i, \textbf x_j) \end{equation} where \(G(\textbf x,\textbf y)\) is the Coulomb or the screened Coulomb potential, defined respectively by \begin{equation} \label{eq_CP} G_0(\textbf x, \textbf y)=\frac{1}{4\pi|\textbf x-\textbf y|} \end{equation} and \begin{equation} \label{eq_sCP} G_\kappa(\textbf x, \textbf y)=\frac{e^{-\kappa |\textbf x-\textbf y|}}{4\pi|\textbf x-\textbf y|}. \end{equation} Note we attempted to use CGI units here but supply the additional \(4\pi\) coefficient in the denominator to represent electrostatic potential generated from partial charges with units of fundamental charges, as from most force field generators such as CHARMM and AMBER.

Particle-cluster interaction

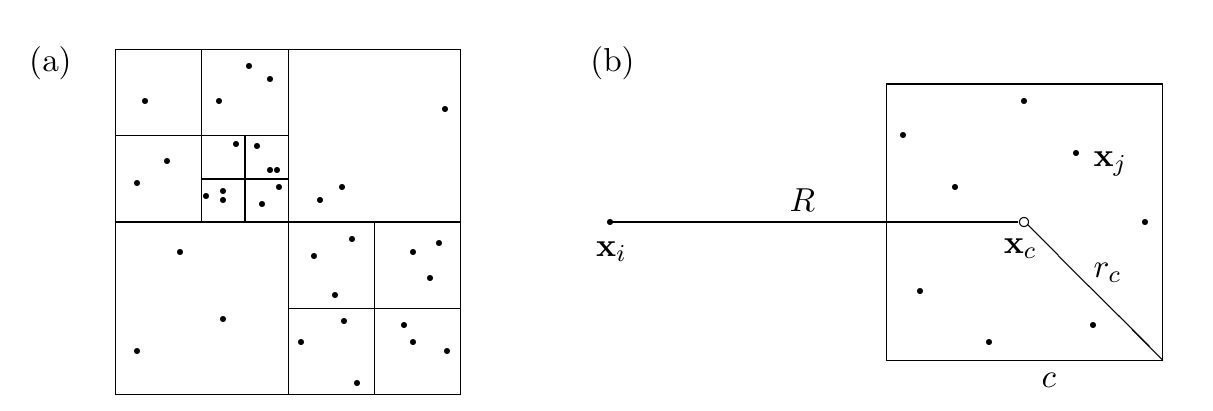
We assume that the particles have been partitioned into a hierarchy of clusters as illustrated in above Figure (a). In the partition process, each cluster (a rectangle in 2-D or a rectangular parallelepiped in 3-D) is divided into four (or eight for 3-D) sub-clusters until the pre-determined treecode parameter \(N_0\), the maximum number of particles per leaf (a cluster without sub-clusters), is satisfied. Here we illustrate in 2-D using \(N_0=3\); the more practical 3-D case is similar. %(the procedure will be described later). Treecode evaluates the potential in Eq.~(\ref{particle-particle}) as a sum of particle-cluster interactions, \begin{equation} \label{particle_cluster_form} V_i = \sum_c V_{i,c}, \end{equation} where \begin{equation} \label{particle_cluster} V_{i,c} = \sum_{\textbf y_j \in c} q_j\, G(\textbf x_i,\textbf y_j) \end{equation} is the interaction between a target particle $\textbf x_i$ and a cluster of sources \(c=\{\textbf y_j\}\). A particle-cluster interaction is shown schematically in above figure (b): the cluster center, \(\textbf y_c\), is the geometric center of the rectangle; \(R\) is the particle-cluster distance; and the cluster radius, \(r_c\), is the distance from $\textbf y_c$ to one of the vertices of the rectangle.

The treecode algorithmn has two options for computing a particle-cluster interaction \(V_{i,c}\). It can use direct summation as in the definition Eq.~(\ref{particle_cluster}) . In practice, the Taylor approximation is used if the following criterion is satisfied, \begin{equation} \label{mac} \frac{r_c}{R}\leq \theta, \end{equation} where \(\theta\) is a user-specified Maximum Acceptance Criterion (MAC) parameter for controlling the error. If the criterion is not satisfied, the code examines the children or sub-clusters of cluster \(c\), or it performs direct summation if \(c\) is a leaf of the tree.

While this discussion has focused on the problem of evaluating the electrostatic potential \(V_i\), similar considerations apply to computations of the electric field \(E_i = -\nabla V_i\), where treecode can also be applied.